KUBUS
·
Unsur-unsur
kubus
·
Diagonal
kubus
·
Cara
melukis kubus
·
Kerangka
kubus
·
Jaring-jaring
kubus
·
Luas
permukaan kubus
·
Volume
kubus
KUBUS
I.
Unsur-Unsur Kubus
a. Sisi
kubus : bidang ABCD
bidang EFGH
bidang ABFE
bidang CDHG
bidang BCGF
bidang ADHE
b. Rusuk
kubus : AB, BC, CD, AD, AE, BF, CG, DH,
EF, FG, GH, EH
Rusuk-rusuk yang sejajar pada kubus :
AB//DC//EF //HG
AD// BC// FG//EH
AE//
BF//CG// DH
c. Titik
sudut : A, B, C, D, E, F, G, H
II.
Diagonal pada Kubus
a. Diagonal
bidang
Diagonal bidang adalah ruas garis yang
menghubungkan dua titik sudut yang berhadapan pada setiap sisi kubus
Diagonal
bidang kubus ABCDEFGH adalah :
AC,
BD, FH, GE, BE, AF, DG, CH, BG, CF, AH, DE
b. Diagonal
ruang
Diagonal
ruang kubus ABCDEFGH adalah : BH,
CE, AG, DF
c. Bidang
diagonal
Bidang
diagonal adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang
pada kubus.
Bidang diagonal kubus ABCDEFGH
adalah :
BDHF, ACGF, ABGH, CDEF, ADGF,
BCHE
III.
Cara
Melukis Kubus
Langkah-langkah melukis kubus :
a.
Lukislah dua buah
persegi, sebagai bagian sisi depan dan sisi belakang kubus. Rusuk yang tidak
terlihat dari depan lukislah dengan garis putus-putus. Perhatikan gambar di
bawah ini.
b.
Hubungkan
rusuk-rusuk dari depan ke belakang. Terbentuklah sebuah kubus.
IV.
Kerangka
Kubus
Sebuah kubus memiliki 12 rusuk.
Jika panjang rusuk kubus adalah s
maka jumlah panjang rusuknya adalah 12s.
Contoh soal :
a.
Panjang
rusuk kubus adalah 5cm. Tentukan jumlah panjang rusuk kubus tersebut!
Penyelesaian :
Jumlah panjang rusuk = 12s
=
12 x 5 cm
=
60 cm
b.
Nadia
mempunyai kawat yang panjangnya 180cm. Dia ingin membuat kerangka kubus. Berapa
panjang rusuk kubus agar kawat tersebut tidak tersisa?
Penyelesaian :
Panjang rusuk = 180 : 12 cm
=
15 cm
V.
Jaring-Jaring
Kubus
Jaring-jaring kubus ada 11 yaitu
:
Contoh soal :
a.
Perhatikan
jarring-jaring kubus di bawah ini. Jika nomer 3 sebagai alas kubus, nomor
berapakah yang merupakan tutup kubus?
Jawab :
untuk
mempermudah menjawab soal tersebut, buatlah jarring-jaring tersebut pada kertas
lalu gunting. Susun menjadi sebuah kubus, sehingga akan diperoleh tutup kubus
adalah nomor 5.
b.
Diketahui
kubus KLMNOPQR. Lengkapilah titik-titik pada jaring-jaring di bawah ini.
VI.
Luas
Permukaan Kubus
Luas
permukaan kubus adalah jumlah luas sisi-sisi kubus. Kalian ingat bahwa kubus
mempunyai 6 sisi dengan panjang rusuk (s). Sedangkan sisi kubus merupakan
bangun datar yaitu persegi. Jadi, untuk mencari luas permukaan kubus adalah 6
kali luas persegi. Atau dengan rumus :
L = 6s2
|
Keterangan :
L = luas permukaan kubus
s = panjang rusuk kubus
Contoh
soal :
a.
Berapakah
luas permukaan kubus yang mempunyai panjang rusuk 12cm ?
Penyelesaian
:
L =
6s2
= 6 x 12 x 12 cm2
= 864 cm2
b.
Dua
buah kubus mempunyai panjang rusuk masing-masing 5 cm dan 10 cm. Berapakah perbandingan luas permukaan
dua kubus tersebut?
Penyelesaian
:
L1 = 6 x 5 x 5 cm2
= 150 cm2
L2 = 6 x 10 x 10 cm2
= 600 cm2
Jadi,
L1 : L2 = 150 : 600 = 1 : 4
VII.
Volume
Kubus
Kubus di samping
mempunyai 8 kubus kecil. Kubus-kubus kecil tersebut merupakan isi/volume kubus
besar.
Dengan
kata lain, volume kubus di samping adalah
2
satuan x 2 satuan x 2 satuan = 8 satuan
V = rusuk x rusuk x rusuk
= s x s x s
= s3
|
Keterangan
:
V =
volume kubus
s =
panjang rusuk
Contoh
soal :
a.
Sebuah
bak mandi berbentuk kubus mempunyai panjang rusuk 1,5 m. Berapakah volume bak
mandi tersebut? (dalam cm)
Penyelesaian :
s = 1,5 m = 150 cm
V = s3
=
150 x 150 x 150 cm3
=
3375000 cm3
b.
Diketahui
luas permukaan sebuah kubus 294 cm2. Hitunglah volume kubus
tersebut!
Penyelesaian :
L =
294
L = 6s2
6s2 = 294
s2 = 49
s = 7
V = s3
= 7 x 7 x 7 cm3
=
343 cm3
sumber : http://ajar-matematika.blogspot.com/2012/10/kubus-smp-kelas-viii.html
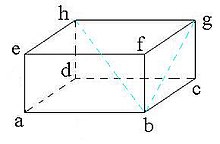
Balok
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang,
dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok
memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh
enam persegi sama dan sebangun disebut sebagai kubus.
|
|
Elemen balok
- Panjang
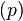 adalah rusuk terpanjang dari alas balok.
adalah rusuk terpanjang dari alas balok. - Lebar
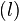 adalah rusuk terpendek dari sisi alas balok.
adalah rusuk terpendek dari sisi alas balok. - Tinggi
 adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.
adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.
Rumus balok
Luas permukaan

Volume

Panjang diagonal ruang

Panjang diagonal bidang



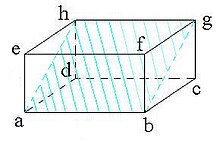
Luas bidang diagonal



sumber : http://id.wikipedia.org/wiki/Balok













Tidak ada komentar:
Posting Komentar